Question

Solve this inequality

Answer 1

`\boxed{ \large\displaystyle\text{$\begin{gathered}\sf \bf{-8\leq 10-2x < 28 } \end{gathered}$} }`

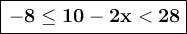
Separate the inequality compound in the inequality system.

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{{\left\{ \begin{array}{r}10-2x\geq -8 \\ 10-2x < 28 \ \end{array} \right.} } \end{gathered}$} }`

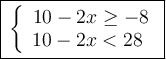
We solve to: 10 - 2x < 28

Order the unknown terms to the left side of the equation.
`\boxed{\bf{-2x < 28-10 }}`

Calculate the sum or difference.

`\boxed{\bf{-2x < 18 }}`

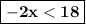
Divide both sides of the equation by the coefficient of the invariable.
`\boxed{\bf{x > -(18)/(2) }}`

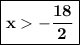
Clear the common factor

`\boxed{\bf{x > -9} }}`

We solve to: 10 - 2x ≥ -8

Order the unknown terms to the left side of the equation.

`\boxed{\bf{-2x\geq -8-10 }}`

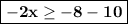
Calculate the sum or difference.

`\boxed{\bf{-2x\geq -18 }}`

Divide both sides of the equation by the coefficient of the invariable.

`\boxed{\bf{x\leq (-18)/(-2) }}`

Determine the sign of multiplication and division.

`\boxed{\bf{x\leq (18)/(2) }}`

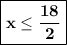
Clear the common factor

`\boxed{\bf{x\leq 9}}`

`\boxed{ \large\displaystyle\text{$\begin{gathered}\sf \bf{x > -9 \ and \ x\leq 9 } \end{gathered}$} }`

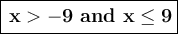
We find the intersection.

Answer =
`\boxed{ \large\displaystyle\text{$\begin{gathered}\sf \bf{-9 < x\leq 9 } \end{gathered}$} }`

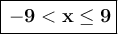
Alternative forms: x ∈ (-9, 9]