Question

Which graph represents the solution of −2⁢x≤4⁢(x−6)?

Answer 1

See attachments.

Explanation:

Given inequality:

`-2x\leq 4(x-6)`

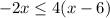
Solve the inequality by first expanding the brackets:

`\implies -2x\leq 4x-24`

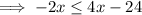
Subtract 4x from both sides:

`\implies -2x-4x\leq 4x-24-4x`

`\implies -6x\leq -24`

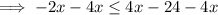
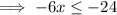
Divide both sides by -6 (remembering to reverse the inequality sign as we are dividing by a negative number).

`\implies (-6x)/(-6)\leq (-24)/(-6)`

`\implies x\geq 4`

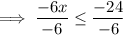
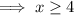
When graphing inequalities on a coordinate plane:

• < or > : dashed line.
• ≤ or ≥ : solid line.
• < or ≤ : shade under the line.
• > or ≥ : shade above the line.

Therefore, to graph the given inequality on a coordinate plane:

• Draw a solid line at x = 4.
• Shade above the line (i.e. shade to the right of the line).

(See attachment 1).

When graphing inequalities on a number line:

• < or > : open circle.
• ≤ or ≥ : closed circle.
• < or ≤ : shade to the left of the circle.
• > or ≥ : shade to the right of the circle..

Therefore, to graph the given inequality on a number line:

• Place a closed circle at 4.
• Shade to the right of the circle.

(See attachment 2).