Question

If f(x) = ln [ sin2(2x)(e-2x+1) ] , then f’(x) is

I want to solve ?

Answer 1

Here we will write our function in regular form using an identity.

• 
  `log(ab)=loga+logb`
• 
  `log(a/b)=loga-logb`

Therefore, the rule of our function
`f(x)` will be as follows.

• 
  `f(x)=ln(sin^2(2x))+ln(e^(-2x)+1)`

The derivative of the natural logarithm
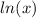`ln(x)` function is of the following form.

• 
  `(ln(x))'=(x')/(x)`

It is found by dividing the derivative of the function in
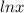`lnx` by the function in
`lnx`.

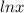For example:

• 
  `(ln(5x))'=((5x)')/(5x) =(5)/(5x) =(1)/(x)`

According to this information, let's take the derivative of our function.

• 
  `f'(x)=(2sin(4x))/(sin^2(2x)) +(-(2)/(e^(2x)) )/(e^(-2x)+1)`
• 
  `f'(x)=4cot(2x)-(2)/(1+e^(2x))`

Rules:

• 
  `((sin2x)²)'=2.2sin(2x)cos(2x)=2sin(4x)`
• 
  `(e^x)'=x'.e^x`