Answer: x = 4
======================================================
Work Shown:
As you mentioned, we'll use Pythagoras' Theorem aka Pythagorean Theorem.
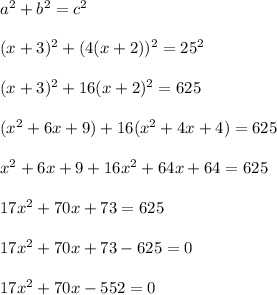
Next, we'll use the quadratic formula with a = 17, b = 70, c = -552.

Ignore the negative x value solution. The sides (x+3) and 4(x+2) will be negative values if we plugged in x = -8.1176, but negative side lengths do not make sense.
This makes x = 4 the only possible solution.
----------------
If x = 4, then,
- vertical leg = x+3 = 4+3 = 7
- horizontal leg = 4(x+2) = 4*(4+2) = 4*6 = 24
This is a 7-24-25 right triangle.
We can confirm this using the pythagorean theorem
