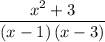Answer:
B.
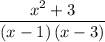
Explanation:
Will provide explanation later since you are in a hurry
1. Find the LCM of the two denominators: x-1 and x -3
This is (x-1)(x-3)
2. Multiply each numerator by the same amount needed to multiply itscorresponding denominator to turn it into the LCM (x−1)(x−3)
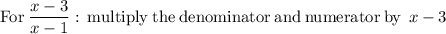
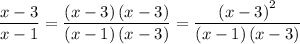
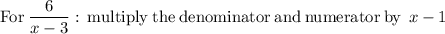
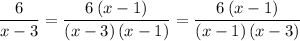
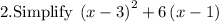
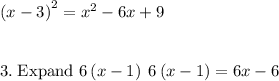
4. Since the denominators are the same in both terms, we can add the numerators and use the common denominator as the denominator for the result
- Adding numerators derived from steps 2 and 3 above we get
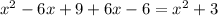
- Dividing by the common denominator (x-1)(x-3) gives the result as