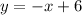Question

Write the equation of the line in a fully simplified slope-intercept form.

Answer 1

Slope Intercept Form From a Graph

Slope intercept form:
`y=mx+b`

• m = slope
• b = y-intercept

We can identify two points on the given graph and solve for the slope and the y-intercept.

Solving the Question

Two clear points on the graph are (6,0) and (0,6).

First, we can solve for the slope by using the slope equation:

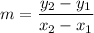`m=(y_2-y_1)/(x_2-x_1)` where two points are
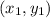`(x_1,y_1)` and
`(x_2,y_2)`

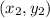
⇒ Plug in the points (6,0) and (0,6):

`m=(0-6)/(6-0)\\\\m=(-6)/(6)\\\\m=-1`

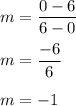
Therefore. the slope of the line is -1. Plug this into
`y=mx+b`:

`y=-x+b`

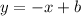
Now, we can find the y-intercept. It is the value of y when the line crosses the y-axis.

In this case, we can see on the graph that this is 6.

`y=-x+6`

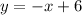
Answer

`y=-x+6`