Answer:
A. 6
Explanation:
Using the Pythagorean theorem which states that: Hypotenus² = Opposite² + Adjacent²
Where: hypotenus = 10, opposite = x, adjacent = 8
So:
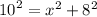
Solving for x
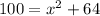
Collect like terms to make x the subject of formula
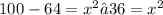
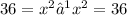
square root both sides of the equation to find the value of x
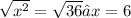
Therefore: Option A is correct