Answer:
No.
Explanation:
Pre-Solving
We are given the following inequality:
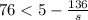
And we want to know if s=2 is a solution, meaning if s is 2, will the inequality still be true?
Solving
We can substitute 2 for s in the inequality to test it.
Replace s with 2.
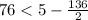
First, let's divide 136 by 2.
136/2 = 68
The inequality is now:
76 < 5 - 68
Subtract 68 from 5.
76 < -63
The inequality reads "76 is less than -63", which is a false statement (76 is positive, -63 is negative, and positive numbers are greater than negative numbers).
Ergo, s = 2 is not a solution to the inequality.