Question

P.L.Z HELP. 50pts

Sal's Sandwich Shop sells wraps and sandwiches as part of its lunch specials. The profit on every sandwich is $2, and the profit on every wrap is $3. Sal made a profit of $1,470 from lunch specials last month. The equation 2x + 3y = 1,470 represents Sal's profits last month, where x is the number of sandwich lunch specials sold and y is the number of wrap lunch specials sold.

Change the equation to slope-intercept form. Identify the slope and y-intercept of the equation. Be sure to show all your work.

Slope-intercept form: y=-2/3=x+490 The slop is -2/3 and the y-intercept is unknown.
Describe how you would graph this line using the slope-intercept method. Be sure to write using complete sentences.

Write the equation in function notation. Explain what the graph of the function represents. Be sure to use complete sentences.

Graph the function. On the graph, make sure to label the intercepts. You may graph your equation by hand on a piece of paper and scan your work or you may use graphing technology.

Suppose Sal's total profit on lunch specials for the next month is $1,593. The profit amounts are the same: $2 for each sandwich and $3 for each wrap. In a paragraph of at least three complete sentences, explain how the graphs of the functions for the two months are similar and how they are different.

Answer 1

`y=-(2)/(3)x+490`

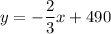
Explanation:

`\boxed{\begin{minipage}{6.3 cm}\underline{Slope-intercept form of a linear equation}\\\\$y=mx+b$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $b$ is the $y$-intercept.\\\end{minipage}}`

Given equation:

`2x + 3y = 1470`

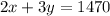
To change the equation to slope-intercept form, isolate y:

`\implies 2x + 3y -2x=1470 -2x`

`\implies 3y=-2x+1470`

`\implies (3y)/(3)=(-2x+1470)/(3)`

`\implies y=-(2)/(3)x+(1470)/(3)`

`\implies y=-(2)/(3)x+490`

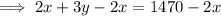
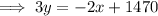
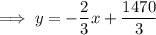
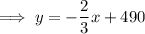
Therefore:

• 
  `\textsf{Slope} =-(2)/(3)`

• 
  `\textsf{$y$-intercept}=490`

To graph this line with the slope-intercept method:

• Plot the y-intercept at (0, 490).
• The slope gives us the change in y-values over the change in x-values (rise over run). Therefore, use the slope to plot the next few points by mapping 3 units to the right and 2 units down each time:
  ⇒ (0+3, 490-2) = (3, 488)
  ⇒ (3+3, 488-2) = (6, 486)

To write the equation in function notation, replace the y-variable for f(x).

`\implies f(x)=-(2)/(3)x+490`

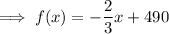
The graph of the function represents:

• The number of wrap lunch specials sold given the number of sandwich lunch specials sold.

The y-intercept of the graph is (0, 490).

To find the x-intercept, set the function to zero and solve for x:

`\implies -(2)/(3)x+490=0`

`\implies -(2)/(3)x=-490`

`\implies -2x=-1470`

`\implies x=735`

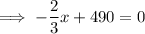
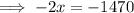
Therefore, the x-intercept is (735, 0).

The graph of the function is attached.

If Sal's total profit on lunch specials for the next month is $1,593 (where the profit amounts are the same) the equation would be 2x + 3y = 1593 and the function would be:

`g(x)= -(2)/(3)x+531`

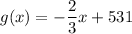
As the coefficient of the x-variable has not changed, the slopes of the two functions are the same.

As the total profit has changed, the intercepts are different.

The y-intercept of the first function is (0, 490) and its x-intercept is (735, 0). Whereas the y-intercept of the second function is (0, 531) and its x-intercept is (796.5, 0).