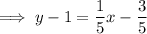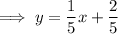Answer:
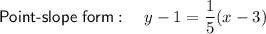
Explanation:
Define the given points:
- (x₁, y₁) = (3, 1)
- (x₂, y₂) = (-7, -1)
Substitute the defined points into the slope formula to find the slope of the line:
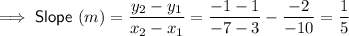
Substitute the found slope and one of the points into the point-slope formula:
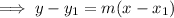
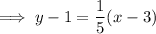
Simplify to slope-intercept form, if necessary: