Question

A 35 foot ladder is set against the side of a house so that it reaches up 21 feet. If Elijah

grabs the ladder at its base and pulls it 4 feet farther from the house, how far up the
side of the house will the ladder reach now? (The answer is not 17 ft.) Round to the
nearest tenth

Answer 1

14.2 feet

Explanation:

Use the Pythagorean Theorem to solve both parts.

Part 1.

35 is the hypotenuse and 21 is a leg.

`a^(2) +b^(2) =c^(2) \\a^(2) +21^(2) =35^2\\a^2 + 441 = 1225\\a^2 +441-441=1225-441\\a^2 =784\\√(a^2) =√(784) \\a = 28 feet`

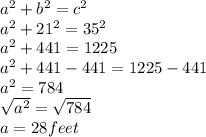
28 feet represents how far the base of the ladder is from the house.

Part 2.

Now move the ladder 4 feet farther from the house. 28 + 4 = 32 ft.

Now you have a leg that is 32 feet and the hypotenuse is still 35 feet. Solve for the other leg.

`a^(2) +b^(2) =c^(2) \\a^(2) +32^(2) =35^2\\a^2 + 1024 = 1225\\a^2 +1024-1024=1225-1024\\a^2 =201\\√(a^2) =√(201) \\a = 14.177 feet`

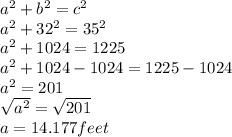
Round to the nearest tenth and you have 14.2 feet