Answer:
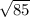
Explanation:
Let's use the distance formula to solve for the distance between the two given points!
d =
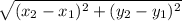
Now, we input the points:
(5-(-2) + (-2-4)
(which will equal...)
(7) + (-6)
Now we input the solutions we got here to the distance formula:
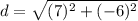
(we simplify....)
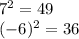
input these solutions into the distance formula again...
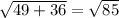
85 is not a number that can be square rooted properly, nor does it have any perfect squares available to divide equally.
Therefore, we conclude that the distance between A(5, -2) and B(-2,4) is
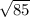 .
.