Answer:
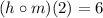
=======================================================
Step-by-step explanation:
The notation
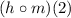 refers to function composition
refers to function composition
It's the same as writing

According to
m = {(3,4), (2,-2), (-2,6), (5,8)}
We have m(2) = -2 since x = 2 leads to m(x) = -2
Then the output -2 is treated as the input of the outer function h(x)
Looking through
h = {(1,5), (-2,6), (4, -3), (6,9)}
shows that h(-2) = 6
Therefore,
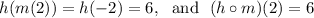
Optionally we can write out a table like shown below.
The row highlighted shows the input x = 2 leading to m(x) = -2, which is then plugged into h(x) to get 6 as the final output. Think of it like a chain of dominoes.