Answer:
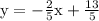
===============================================
Work Shown:
I'll be using point slope form to get these steps
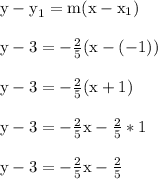
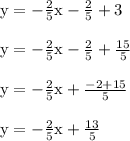
This answer has a slope of -2/5 and y intercept of 13/5.
Parallel lines have equal slopes but different y intercepts.
To verify this equation, plugging in x = -1 leads to y = 3.