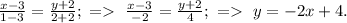Question

Find the equation of a line

Possing through the point (1,2)
A with slope m=3
B) and also
passing through Point (3,-2)

Answer 1

1) A(1;2) and slope=3.

slope-interception form is y=s*x+i, where s - slope, i - interception.

if to substitute the given coordinates and slope into the equation, then 2=3*1+i, ⇒ i=-1. It means, the required equation is:

y=3x-1.

2) A(1;2) and B(3;-2).

the common form is:

`(x-X_B)/(X_A-X_B) =(y-Y_B)/(Y_A-Y_B).`

If to substitute the given coordinates into the common form, then:

`(x-3)/(1-3) =(y+2)/(2+2) ; \ => \ (x-3)/(-2) =(y+2)/(4); \ => \ y=-2x+4.`

Answer 2

Answers:

y=2x2−20x+51

Explanation:

Vertex:

(5,1)

Focus:

(5,98)

Axis of Symmetry:

x=5

Directrix:

y=78