Question

Show that the two triangles are congruent. PLs help

Answer 1

Ignore the angles of triangle DEF. They complicate things when they don't need to be like that.

The distance from E to F is 3 units since there are 3 spaces between the points. Or you could subtract the x coordinates of each point, so 7-4 = 3.

So far we have one pair of congruent sides

EF = BC = 3

----------------------

Let's use the distance formula to find the distance from D to E

`D = (x_1,y_1) = (3,-1) \text{ and } E = (x_2, y_2) = (7,-4)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((3-7)^2 + (-1-(-4))^2)\\\\d = √((3-7)^2 + (-1+4)^2)\\\\d = √((-4)^2 + (3)^2)\\\\d = √(16 + 9)\\\\d = √(25)\\\\d = 5\\\\`

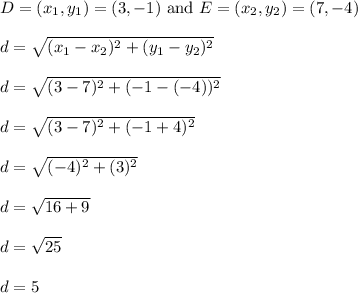
Segment DE is exactly 5 units long.

We have another pair of congruent sides between the two triangles

AB = DE = 5

----------------------

We'll use the distance formula one last time to find the length of side FD.

`D = (x_1,y_1) = (3,-1) \text{ and } F = (x_2, y_2) = (4,-4)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((3-4)^2 + (-1-(-4))^2)\\\\d = √((3-4)^2 + (-1+4)^2)\\\\d = √((-1)^2 + (3)^2)\\\\d = √(1 + 9)\\\\d = √(10)\\\\√(10) \approx 3.162278 \approx 3.2\\\\`

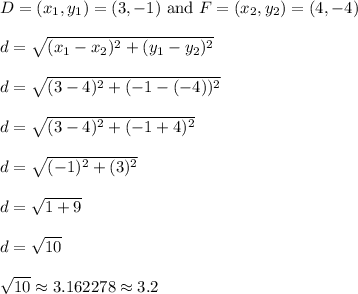
Side FD is approximately 3.2 units long, which matches with AC = 3.2

--------------------

Here are the three paired sides that are congruent to one another

• AB = DE = 5
• BC = EF = 3
• AC = FD = 3.2 approximately

Since we have three pairs of congruent sides, we can use the SSS (side side side) congruence theorem to prove the triangles are congruent.

Congruent triangles are identical copies or clones of one another. One triangle is just a reflected and translated version of the other.

This means they have the same corresponding angle measures, and the same corresponding side lengths.