Question

Segment RS is translated by (x+1, y-2) and then reflected over the x-axis. The resulting segment R" S" has coordinates R" (7,3) and

S" (2,7). What are the coordinates of the segment RS?

can someone pls help meee

Answer 1

Answers:

R = (6, -1)

S = (1, -5)

==========================================================

Step-by-step explanation:

R'' is located at (7,3)

Reflect this over the x axis to get R'(7,-3). We flip the sign of the y coordinate while keeping the x coordinate the same. The rule is
`(x,y) \to (x,-y)`

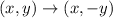
Then we apply the inverse of (x+1, y-2) which is (x-1, y+2). Notice the sign flips.

Let's apply this inverse transformation to determine the coordinates of point R.

`(\text{x},\text{y})\to(\text{x}-1,\text{y}+2)\\\\(7,-3)\to(7-1,-3+2)\\\\(7,-3)\to(6,-1)\\\\`

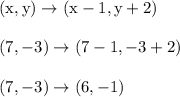
Therefore, point R is located at (6, -1)

-------------------

Point S'' is at (2,7)

It reflects over the x axis to get to (2,-7)

Then we apply that inverse transformation to get

`(\text{x},\text{y})\to(\text{x}-1,\text{y}+2)\\\\(2,-7)\to(2-1,-7+2)\\\\(2,-7)\to(1,-5)\\\\`

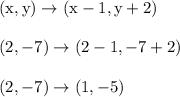
Point S would be located at (1, -5)