Question

NO LINKS!! Part 3: Please help me with this Similarity Practice​

Answer 1

C' = (10, 5)

Dilation by a scale factor of 2 with the origin (0, 0) as the center of dilation, followed by a translation of 1 unit up.

Step-by-step explanation:

If two triangles are said to be similar, their corresponding angles are congruent and their corresponding sides are in the same ratio.

Therefore, to maintain similarity (and thus keep the corresponding angles of both triangles the same) but not maintain congruence, dilate triangle ABC.

Given vertices of triangle ABC:

• A = (0, 0)
• B = (1, 4)
• C = (5, 2)

Given vertex of triangle A'B'C':

• B' = (2, 9)

If ΔABC is dilated by a scale factor of 2, with the origin as the center of dilation, B' = (2, 8). If the triangle is then translated 1 unit up, B' = (2, 9), which matches the given coordinate of point B'.

Therefore, the series of transformations is:

• Dilation by a scale factor of 2 with the origin (0, 0) as the center of dilation.
• Translation of 1 unit up.

Mapping Rule: (x, y) → (2x, 2y + 1)

Therefore, the coordinates of point C' are:

⇒ C' = (2(5), 2(2) + 1) = (10, 5)

Answer 2

Answer: (10,5) or (14,3) are two possible answers.

Infinitely many answers are possible. Pick one to write as the final answer to your teacher.

=====================================================

Step-by-step explanation:

Focus on the points B(1,4) and C(5,2)

More specifically, focus on the x coordinates 1 and 5. To go from B to C, we move to the right 4 units since 1+4 = 5

We also move down 2 units since we go from y = 4 to y = 2

In short, the translation motion is "right 4, down 2". We can further abbreviate this into the vector notation <4, -2>. This translation vector only applies going from B to C.

The vector notation <4,-2> is the same as writing
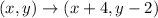`(x,y) \to (x+4,y-2)` but the first method is much faster to write out since it avoids needing to write x or y.

--------------------

Now if we want to construct a similar triangle A'B'C', we will use that vector to scale it up or down. Let's scale it up and double each coordinate.

<4, -2> doubles to <8,-4>

So instead of "right 4, down 2" we now follow the path "right 8, down 4". Take notice how both motions involve the same slope.

Start at B'(2,9) and move right 8 and down 4 to arrive at C'(10,5)

See figure 1 below.

This is one possible answer out of infinitely many. This is because we can change the scale factor to any nonnegative real number we want.

-------------------

Another example:

Instead of doubling the coordinates of the translation vector, let's triple them.

<4,-2> triples to <12,-6>

Then start at B'(2,9) and move right 12 and down 6 to arrive at C'(14,3) which is another possible answer out of infinitely many.

See figure 2 below.

Pick whichever of (10,5) or (14,3) is your favorite to get the final answer, assuming your teacher wants you to write one (x,y) location only. Or pick some other scale factor (other than 2 or 3) and follow the same idea to get some other possible location of point C'.