Question

Steps
Area of a circle = 9π
radius = x-4

Answer 1

The radius of the circle is 3 units.

Explanation:

1. Write the formula for the area of a circle.

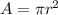`A=\pi r^(2)`; where A is the area of the circle and r is the radius of said circle.

2. Substitute the given values into the formula.

`(9\pi )=\pi (x-4)^(2)`

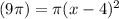
3. Expand the parenthesis (check attched image 1).

`(9\pi )=\pi ((x)^(2)-2(x)(4)+(4)^2 )`

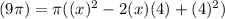
4. Simplify and solve the parenthesis.

`(9\pi )=\pi (x^(2)-8x+16)\\`

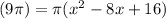
5. Solve for x.

`(9\pi )/(\pi ) =(x^(2)-8x+16)\\\\ \\9 =x^(2)-8x+16`

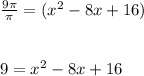
6. Move all terms to one sode of the equation.

`x^(2)-8x+16-9=0\\ \\x^(2)-8x+7=0`

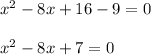
7. Use the formula for solving quadratic equations (check attached image 2).

To find the values of a, b and c, take the coefficient of the variables when the equation is written in descending order of exponents.

a= 1 (because the coefficient of
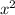`x^2` is 1)

b= -8 (because the coefficient of
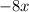`-8x` is 1)

c= 7 (because the coefficient of 7 is itself).

`x_(1)=\frac{-(-8)+\sqrt{(-8)^(2)-4(1)(7) } }{2(1)} =7\\ \\x_(2)=\frac{-(-8)-\sqrt{(-8)^(2)-4(1)(7) } }{2(1)} =1`

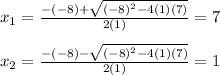
Finding these 2 solutions for the equation indicates that of we plug in this values in the initial "r" formula (x-4) we can get the radius dimension of this circle.

8. Find the dimension.

To find the radius of the circle, take the solutions of the equatiobs and calculate:

`r_(1) =(1)-4=-3\\\\ r_(2) =(7)-4=3`

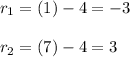
These 2 are the possible dimensions of our radius, but, since a dimension cannot be expressed as a negative number, we can only take the positive solution.

9. Express your result.

The radius of the circle is 3 units.