Question

Find the points on
y = x³ + 6x² - 15x + 1 at which the
gradient is zero.

Answer 1

(-5, 101) or (1, -7)

Explanation:

The gradient of a function is zero when its first differential is zero

Taking first derivative of y = x³ + 6x² - 15x + 1

we get

`(dy)/(dx) = (d)/(dx)(x^3+6x^2-15x\:+\:1)`

`= (d)/(dx)(x^3)+ (d)/(dx)(6x^2) - (d)/(dx)(15x)\:+\: (d)/(dx)(1)\\\\`

`= 3x^2 + 2(6x) - 15 + 0\\\\\\= 3x^2 + 12x - 15x\\`

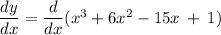
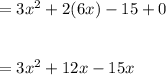
Set this first differential to 0, find the solution set for x

`3x^2 + 12x - 15x =0`

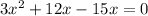
This is a quadratic equation which will have 2 solutions for x.

First divide throughout by 3

`= > x^2 + 4x - 5 = 0`

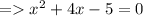
Factor the term:

`= > x^2 + 4x - 5 = 0\\\\== > (x -1)(x + 5) = 0\\== > x - 1 =0 \text { or } x + 5 =0\\\\`

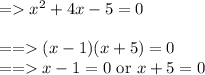
This means x = 1 or x = -5 is the solution set

To find the y value corresponding to these values of x, plug in each of these x values in the original equation and solve for y

Plug in x = 1 into equation x³ + 6x² - 15x + 1

=> 1³ + 6(1)² - 15(1) + 1

=> 1 + 6 - 15 + 1

=> -7

So one point is (1, -7)

Looking at the choices we can eliminate the first and last choices

Looking at choices 2 and 3 we see that only one of them has x = -5 which is the other solution value. This is the second choice

So the correct answer is second choice
(-5, 101) or (1, -7)

Note we did not have to go through the pain of computing y for x = -5