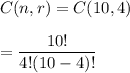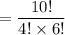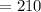Question

The bowling team at Lincoln High School must choose a president, vice president, and secretary. If the team has 10 members, how many ways could the officers be chosen?

Answer 1

210 ways

Explanation:

This is a combinatorics problem of the general nature of choosing r elements from a sample of n elements

It is indicated by the term

`C(n,r) = $\displaystyle \binom{n}{r} = (n!)/(( r! (n - r)! )$)\\\\`

where n! represents the factorial of n = n x (n-1) x (n-2) x .... 3 x 2 x 1

With n = 10, r = 3 there are C(10, 3) ways of choosing the officers

`C(n,r) = C(10,4)\\\\= (10!)/(4! (10 - 4)! )\\\\\\`

`= (10!)/(4! * 6! )`

`$\displaystyle = 210`