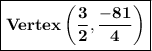Answer:
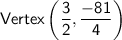
Explanation:
Vertex of quadratic function:
- Write the equation in vertex form by using the method completing the square.
y = x² - 3x - 18
Add 18 to both sides.
y + 18 = x² - 3x
Divide the co-efficient of x by 2 and square the result and then add it to both sides.
Co-efficient of x = 3. Divide 3 by 2and add (3/2)² to both sides
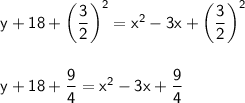
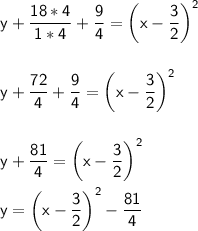
Vertex form: f(x) = (x - h)² + k
where h and k are the vertex co-ordinates.