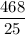Answer:
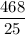
Explanation:
We are asked to find
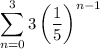
We are asked to find s₄ which is the sum of the first 4 terms of the series. Since n starts at 0, this would be
a₀ + a₁ + a₂ + a₃
We can compute the individual terms and add them up
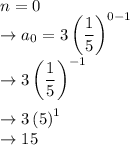
This would be the first term of the geometric sequence
n = 1
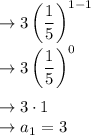
n = 2
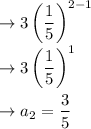
n = 3
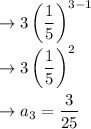
Adding these we get
15 + 3 + 3/5 + 3/25 =
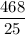
Alternate route
In a geometric sequence the sum of the formula for the first n terms will be
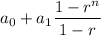
We computed a₀ as 15 and a₁ as 3
So sum
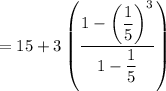
If you evaluate this, it should work out to the same fraction: