Answer:
Range = {-7, -3, 3, 7}
See the attachment for the graph of the function.
Explanation:
The domain of a function is the set of all possible input values (x-values).
The range of a function is the set of all possible output values (y-values).
Given function: h(x) = 2x + 1
Given domain: {-4, -2, 1, 3}
To find the range of the function, input the values of the domain into the function to calculate the corresponding y-values.
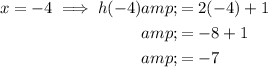
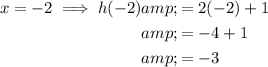
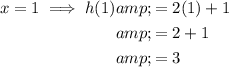
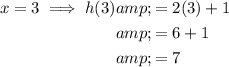
Therefore, the range of the given function is {-7, -3, 3, 7}.
To graph the function:
- Plot the ordered pairs: (-4, -7), (-2, -3), (1, 3), (3, 7).
- Draw a straight line through the plotted points.
(See attachment).