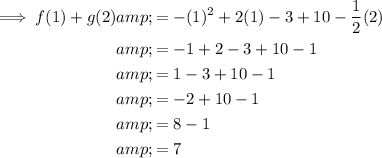Question

I need help with this problem

Answer 1

f(1) + g(2) = 7

Explanation:

Given functions:

`\begin{cases}f(x)=-x^2+2x-3\\g(x)=10-(1)/(2)x \end{cases}`

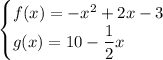
To find f(1), substitute x = 1 into function f(x):

`\begin{aligned}x=1 \implies f(1)& =-(1)^2+2(1)-3\\& = -1+2-3\\&=1-3\\&=-2\end{aligned}`

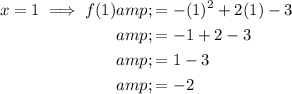
To find g(2), substitute x = 2 into function g(x):

`\begin{aligned}x=2 \implies g(2)& =10-(1)/(2)(2)\\& =10-1\\&=9\end{aligned}`

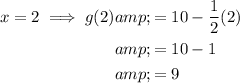
Therefore, to evaluate f(1) + g(2), sum the two values found for f(1) and g(2):

`\begin{aligned}\implies f(1)+g(2)&=-2+9\\&=7\end{aligned}`

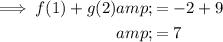
As one calculation:

`\begin{aligned}\implies f(1)+g(2)&=-(1)^2+2(1)-3+10-(1)/(2)(2)\\&=-1+2-3+10-1\\&=1-3+10-1\\&=-2+10-1\\&=8-1\\&=7\end{aligned}`