Answer:
(x, y) → (x + 4, y - 3)
h = 4
k = -3
Explanation:
Given points:
- M = (3, 4)
- M' = (7, 1)
- T = (-2, 3)
- T' = (2, 0)
Given translation:
(x, y) → (x+h, y+k)
To find the value of h, subtract the x-values of points M and T from the x-values of points M' and T':
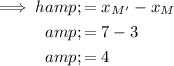

To find the value of k, subtract the y-values of points M and T from the y-values of points M' and T':
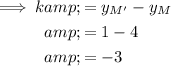
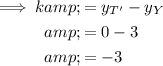
Therefore the algebraic description of the translation is:
(x, y) → (x + 4, y - 3)