Question

1..A message in a bottle is floating on top of the ocean in a periodic manner. The time between periods of maximum heights is 26 seconds, and the average height of the bottle is 12 feet. The bottle moves in a manner such that the distance from the highest and lowest point is 6 feet. A cosine function can model the movement of the message in a bottle in relation to the height.

Part A: Determine the amplitude and period of the function that could model the height of the message in a bottle as a function of time, t. (5 points)


Part B: Assuming that at t = 0 the message in a bottle is at its average height and moves upwards after, what is the equation of the function that could represent the situation? (5 points)


Part C: Based on the graph of the function, after how many seconds will it reach its lowest height? (5 points)


Show/Explain answer for each Part for the answer please

Answer 1

See below for answers and explanations (along with a graph attached)

Explanation:

Part A

The amplitude of a sinusoidal function is half the distance between the maximum and the minimum. It is given to us that the distance from the highest and lowest point is 6 feet, so our amplitude is 6/2 = 3 feet

Part B

The graph's function would be in the form of
`y=acos(bx+c)+d` where
`a` is the amplitude,
`(2\pi)/(b)` is the period,
`-(c)/(b)` is the phase/horizontal shift, and
`d` is the average/midline.

We already know our amplitude of
`a=3` from part A.

Since our period is given to us as 26 seconds, then we can use the equation
`(2\pi)/(b)=26` to find
`b`, which happens to be
`b=(\pi)/(13)`.

Since the cosine function starts at its maximum and we want it to start at the average where the bottle travels up, we would need to use the cofunction identity
`sin(x)=cos(x-(\pi)/(2))` which shifts the cosine graph
`(\pi)/(2)` units to the right. This means that
`c=-(\pi)/(2)`, making our phase shift
`-(c)/(b)=-(-(\pi)/(2))/((\pi)/(13))=6.5`, or 6.5 feet to the right

Our average/midline would be
`d=12` as given as the average height by the problem.

Therefore, the function is
`f(x)=3cos((\pi)/(13)x-(\pi)/(2))+12`

Part C

Using our determined function from Part B, by looking at its graph, we see that the bottle will reach its lowest height of 9 feet after 19.5 seconds (see attached graph).

Answer 2

Part A

The distance from the highest and lowest point is 6 feet. Cut this in half to find the amplitude: 6/2 = 3. The amplitude represents the vertical distance from the midline (aka average height) to either the peak or valley points.

The period is 26 seconds because this is the time difference from one max height to the next max height. This is one of a few ways to measure a full cycle. Another way is from min height to the next min height.

Answers:

Amplitude = 3 feet

Period = 26 seconds

==========================================================

Part B

In this case, the template for cosine is

h = Acos(B(t-C))+D

We found the amplitude A = 3 from the previous section.

The period is T = 26 which means B = 2pi/T = 2pi/26 = pi/13

D = 12 because the average height is 12 feet. The average height is always on the midline.

We are told that t = 0 leads to h = 12, so,

`h = A\cos\left(B\left(t-C\right)\right)+D\\\\h = 3\cos\left((\pi)/(13)\left(t-C\right)\right)+12\\\\12 = 3\cos\left((\pi)/(13)\left(0-C\right)\right)+12\\\\3\cos\left((\pi)/(13)\left(-C\right)\right) = 0\\\\\cos\left((\pi)/(13)C\right) = 0\\\\`

Let's isolate the C term

`\cos\left((\pi)/(13)C\right) = 0\\\\(\pi)/(13)C = \arccos(0)\\\\(\pi)/(13)C = (\pi)/(2)\\\\C = (\pi)/(2)*(13)/(\pi)\\\\C = (13)/(2)`

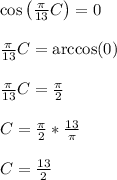
Answer:
`h = 3\cos\left((\pi)/(13)\left(t-(13)/(2)\right)\right)+12\\\\`

==========================================================

Part C

A full period is 26 seconds.

At t = 0 the bottle is at a height of 12 feet

26 seconds later, the bottle is back again at 12 feet to repeat another cycle indefinitely.

At every quarter cycle, the object is either at a min point, max point, or at the average (midline).

So every 26/4 = 6.5 seconds the object will be in one of those places.

In this case, the object starts at 12 feet, goes up to the max 15 feet when t = 6.5

Then another 6.5 seconds later it's back to the midline again. Another 6.5 seconds later (total time is now 6.5*3 = 19.5 seconds) the bottle dips down to the min height of 9 feet. You should see that (19.5, 9) is one of the infinitely many minimum points on this particular cosine curve.

Answer: 19.5 seconds