Answer:
The discriminant is greater than 0, so there are two real roots.
Explanation:

Given equation:
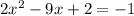
Add 1 to both sides of the equation so that the equation equals zero:
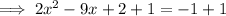
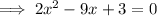
Compare the equation with ax²+bx+c=0:
Substitute the values of a, b and c into the discriminant formula and solve:
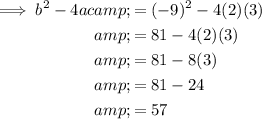
As 57 > 0, the discriminant is greater than zero, so there are two real roots.