The value of x = 7.5 units
The value of y= 12.99 units
The image shows a right triangle with a 60° angle, indicating that this is a 30°-60°-90° special right triangle. In such triangles, the sides are in a consistent ratio: the length of the side opposite the 30° angle is half that of the hypotenuse, and the length of the side opposite the 60° angle is
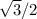 times the length of the hypotenuse.
times the length of the hypotenuse.
Given that the hypotenuse (the side opposite the 90° angle) is 15, we can find x (the side opposite the 30° angle) and y (the side opposite the 60° angle) using the following steps:
1. Find x : Since x is opposite the 30° angle,
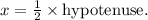
2. Find y : Since y is opposite the 60° angle,
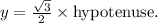
Now we'll calculate these values.
In the 30°-60°-90° triangle given, the lengths of sides x and y are:
- x (opposite the 30° angle) is
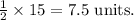
- y (opposite the 60° angle) is
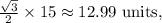 when rounded to two decimal places.
when rounded to two decimal places.