Question

Under the pink line is the answer, simply explain the process

Answer 1

Answer:

The function is continuous at a = 5

Step-by-step explanation:

Given:

`18)\text{ }f(x)\text{ = }(2x^2+3x+1)/(x^2+5x);\text{ a = 5}`

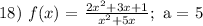
To find:

If the function is continuous at a = 5

For a function to be continuous at a point, the limit exists for the point and the value of the function at that point must be equal to the limit at the point.

when x = 5

`\begin{gathered} f(x)\text{ = }(2(5)^2+3(5)+1)/((5)^2+5(5)) \\ \\ f(x)\text{ = }\frac{50\text{ + 15 + 1}}{25\text{ + 25}} \\ \\ f(x)\text{ = }(66)/(50) \\ \\ f(x)\text{ = }(33)/(25) \end{gathered}`

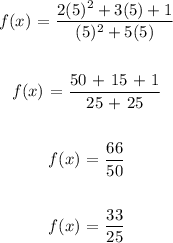
Finding the limit at the point:

`\begin{gathered} \lim_(a\to5)\frac{2x^2+3x\text{ + 1}}{x^2+5x} \\ \\ To\text{ get the limit at the point a = 5, we will susbtitute x with 5} \\ =\text{ }\frac{2(5)\placeholder{⬚}^2+3(5)+1}{(5)\placeholder{⬚}^2+5(5)} \\ \\ =\text{ }(50+15+1)/(25+25)\text{ = }(66)/(50) \\ \\ =\text{ }(33)/(25) \end{gathered}`

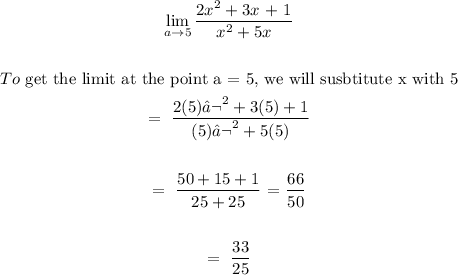
The value of the function at that point is equal to the limit at the point.

Hence, the function is continuous at a = 5