Question

7. An internet service provider charges $20 per month plus an initial set-up fee. One customer paid a total of $92 after 2 months of service. Write an equation in point-slope-form modeling this situation. Then, write the equation in slope-intercept form. What does the 52 represent in your slope-intercept form equation?

Answer 1

The internet service provider charges $20 per month plus an initial set-up fee.

Let "x" represent the number of months that are charged, then the monthly fee can be expressed as 20x

Let "y" represent the cost of the internet service after x months.

If the customer paid y=$92 after x=2 months of service, this information represents a point of the relationship that can be expressed as (2,92)

The point-slope form has the following formula:

`y-y_1=m(x-x_1)`

Where

m is the slope

(x₁,y₁) are the coordinates of one point of the line.

The slope of the line corresponds to the monthly fee for the internet service, so m=$20

The coordinates of the point you have to use is (2,92)

So the equation in point-slope form is

`y-92=20(x-2)`

To write the equation in slope-intercept form, the first step is to distribute the multiplication on the parentheses term:

`\begin{gathered} y-92=20\cdot x-20\cdot2 \\ y-92=20x-40 \end{gathered}`

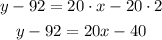
Then pass "-92" to the right side of the equation by adding it to both sides of the equal sign:

`\begin{gathered} y-92+92=20x-40+92 \\ y=20x+52 \end{gathered}`

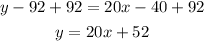
The equation in point-slope form is y-92=20(x-2)

The equation in slope-intercept form is y=20x+52

$20 is the slope of the equation and represents the monthly fee for internet service.

$52 is the y-intercept of the equation, it represents the initial set-up fee for the internet service.