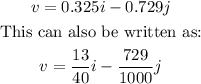Question

Write the vector v in terms of i and j whose magnitude and direction angle are given.

Answer 1

The magnitude, r, of the vector, v , is given to be 4/5.

The direction angle is given to be 114 degrees.

A vector component is written in the form of:

`V=ai+bj`

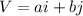
We are going to use the given magnitude and direction angle to obtain the values of a and b.

Thus, we have:

`\begin{gathered} \text{The magnitude, r, of a vector with i and j component is given as:} \\ r=\sqrt[]{a^2+b^2} \\ (4)/(5)=\sqrt[]{a^2+b^2} \\ \text{square both sides;} \\ ((4)/(5))^2=a^2+b^2 \\ (16)/(25)=a^2+b^2 \\ (16)/(25)-b^2=a^2 \\ a^2=(16)/(25)-b^2 \\ a=\sqrt[]{(16)/(25)-b^2}\text{ ----eqn i)} \end{gathered}`
`\begin{gathered} \text{The direction angle, }\theta,\text{ of a vector is given as;} \\ \text{Tan }\theta=(b)/(a) \\ \text{Tan 114=}(b)/(a) \\ -2.2460=(b)/(a) \\ b=-2.2460a\text{ -----eqn }ii) \end{gathered}`

Substitute for b into eqn i); thus we have:

`\begin{gathered} From\text{ eqn i)} \\ a=\sqrt[]{(16)/(25)-b^2} \\ \text{Put b=-2.2460a into the equation, we have:} \\ a=\sqrt[]{(16)/(25)-(-2.2460a)^2} \\ a=\sqrt[]{(16)/(25)-(5.0447a^2)} \\ \text{square both sides;} \\ a^2=(16)/(25)-5.0447a^2 \\ a^2+5.0447a^2=(16)/(25) \\ 6.0447a^2=0.64 \\ a^2=(0.64)/(6.0447) \\ a^2=0.1058 \\ a=\sqrt[]{0.1058} \\ a=0.325 \end{gathered}`

Substitute for a= 0.325 into any of the equations, we have:

`\begin{gathered} \text{From eqn }ii) \\ b=-2.2460a \\ b=-2.2460(0.325) \\ b=-0.729 \end{gathered}`

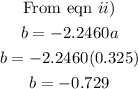
Hence, the vector, v, in terms of i and j is:

`\begin{gathered} v=0.325i-0.729j \\ \text{This can also be written as:} \\ v=(13)/(40)i-(729)/(1000)j \end{gathered}`