ANSWER :
EXPLANATION :
From the problem, we have :
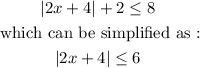
Note that in solving absolute values, the terms inside the absolute value sign can have inverse signs.
Case 1 : Positive
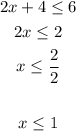
Case 2 : Negative, the symbol will change since we are multiplying a negative number
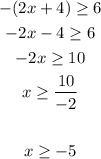
So the solution is :
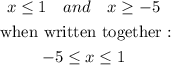
or in interval notation :
[-5, 1]
The graph of it will be :