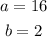To get the answer, we will attempt to simplify the first expression into its simplest format.
![\sqrt[]{(126xy^5)/(32x^3)}](https://img.qammunity.org/2023/formulas/mathematics/college/710qxc0ct0b4nk75z4k5zyjzelu5yubihz.png)
We begin by dividing both the numerator and the denominator by 2:
![\sqrt[]{(63xy^5)/(16x^3)}](https://img.qammunity.org/2023/formulas/mathematics/college/bjne8lyyxigi5ad0v9djgwhcoou5ewcwhw.png)
Since x appears in both the numerator and the denominator, we can simplify such that
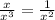
Hence, we have the expression to be
![\sqrt[]{(63y^5)/(16x^2)}](https://img.qammunity.org/2023/formulas/mathematics/college/2g0eka8p8mdtqj79q5g8tlpeks7qp3qmqe.png)
Let us compare the both expressions to each other now:
![\sqrt[]{(63y^5)/(16x^2)}=\sqrt[]{(63y^5)/(ax^b)}](https://img.qammunity.org/2023/formulas/mathematics/college/6ld07pw5f998pl5g0qy1nw1r07b8fn4kx8.png)
Therefore,