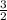Question

Solve the equation with special factors. (Please show all steps)
4p^4 - 25p^2 = -16p^2

Answer 1

p = 0 , p = ±
`(3)/(2)`

Explanation:

4
`p^(4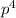)` - 25p² = - 16p² ( add 16p² to both sides )

4
`p^(4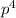)` - 9p² = 0 ← factor out p² from both sides

p²(4p² - 9) = 0 ← factor is a difference of squares

p²(2p - 3)(2p + 3) = 0

Equate each factor to zero and solve for p

p² = 0

p = 0 ( multiplicity of 2 )

2p - 3 = 0 ⇒ 2p = 3 ⇒ p =
`(3)/(2)`

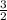
2p + 3 = 0 ⇒ 2p⇒ = - 3 ⇒ p = -
`(3)/(2)`

Answer 2

The solutions can be p=3/2 or p=-3/2

Explanation:

4p^4 - 25p^2 + 16p^2 = 0

4p^4 - 9p^2 = 0

4p^2 - 9p = 0

p^2 = 9/4

p = sqrt(9/4)

p = 3/2 or p = -3/2