SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given probabilities
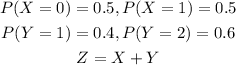
STEP 2: Write the formula for calculating the required probability
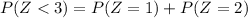
STEP 3: Find P(Z=1)

STEP 4: Find P(Z=2)
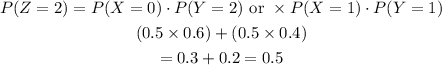
STEP 5: Find the P(Z<3)
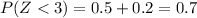
Hence, the answer is 0.7