Question

The half-life of a radioactive kind of uranium is 2 years. How much will be left after 4 years, if you start with 776 grams of it?

Answer 1

194 grams

Step-by-step explanation

We have that the half life of the uranium is 2 years.

This means that it will take 2 years for the uranium to decay to half of its original value.

The formula for exponential decay is:

`y=ab^t`

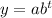
where y = the value after the decay

a = initial value

b = rate of decay.

t = number of years

First, we have to find b.

We have that 776 grams of uranium will decay to half its amount (388 grams) in 2 years. This means that:

`\begin{gathered} 388\text{ = 776 }\cdot b^2 \\ \Rightarrow b^2\text{ = 388 / 776} \\ b^2\text{ = 0.5} \\ b\text{ = }\sqrt[]{0.5} \\ b\text{ = 0.707} \end{gathered}`

Therefore, after 4 years (t = 4), the amount of uranium left will be:

`\begin{gathered} y\text{ = 776 }\cdot(0.707)^4 \\ y\text{ = 776 }\cdot\text{ 0.25} \\ y\text{ = 194 grams} \end{gathered}`

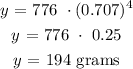
That is the amount of uranium that will be left after 4 years.