Step 1: Rewrite the dot plot in tabular form
Step : Compute the mode
From the table, we can see that the numer appears most ( that is the number with the highest frequence, f) is 4.
Therefore,
mode = 4
Step 3: Find the median
First arrange the data in ascending order. In this case, the data is already in ascending order.
If ∑f is odd, the median is the middle value which is at position

If ∑f is even, the median is the average of the two values at positions
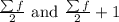
In this case, ∑f = 12 is even.
Therefore, the median is the average of the numbers at position 6 and 7
number at position 6 is 3
number at position 7 is 4
Hence, the median is given by
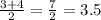
median = 3.5
Step 4: Find the difference between the median and mode
The difference is given by
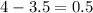
Hence the difference is 0.5