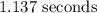Given the model for the height of a ball:
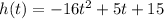
To hit the ground, the height must be h(t) = 0. Then:
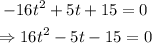
We use the general solution for a quadratic equation:
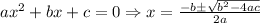
From the problem, we identify:
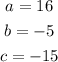
Using the formula:
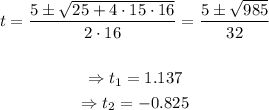
We only take the positive value (because the time is always positive!). Then, the answer is: