Let's draw the figure to better understand the scenario:
To be able to get the measure of ∠WXY, we will be using the relationship of the interior angles of a triangle.
The sum of all interior angles of a triangle is 180°. Therefore we can say,
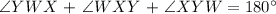
The formula or measure of ∠XYW isn't given. However, we observed that ∠XYW and ∠XYZ are pairs of Supplementary Angles. This means that the sum of two angles is equal to 180°.
We get,
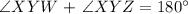
Therefore,
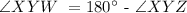
We will use this to complete the formula of the sum interior angles, substituting ∠XYW = 180° - ∠XYZ.
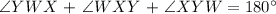
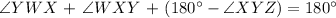
Substituting the given formulas of each angle, let's find x.
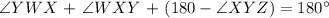
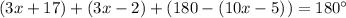
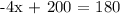
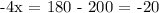
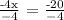
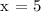
Let's substitute x = 5 to ∠WXY = 3x - 2 to find its measure.
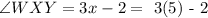
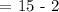
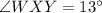
Therefore, the measure of ∠WXY = 13°.