Question

Is 2x-y=44x-2y=6 A Consistent and dependent?

Answer 1

We are given the two equations

`\begin{gathered} 2x-y=4\ldots\ldots\ldots\ldots\ldots\ldots\text{.}(1) \\ 4x-2y=6\ldots\ldots\ldots.\ldots\ldots\text{.}(2) \end{gathered}`

Now, equation (1) x 2

`\begin{gathered} 4x-2y=8\ldots\ldots.\ldots\ldots\ldots\ldots\ldots(1) \\ 4x-2y=6\ldots\ldots\ldots\ldots\ldots\ldots.\ldots(2) \end{gathered}`

Equation (1) - equation (2)

`\begin{gathered} (4x-4x)+(-2y-(-2y))=8-6 \\ 0+0=2 \\ 0=2 \end{gathered}`

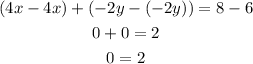
Which is never possible!

Therefore, the system of equation is NOT consistent.

Note:

Let us also draw the graph of the eqautionm given

Therefore, the system of equation is Inconsistent and Independent