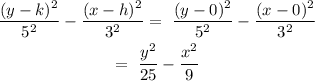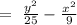
Step-by-step explanation:
The standard form of the hyperbola:
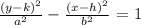
The center of the hyperbola is at (h, k) = The point where the lines intersect
(h, k) = (0, 0)
For hyperbola:
c² = a² + b²
b is gotten by tracing the value of a to the intersecting line. Trace 3 down to the x axis. you get 5.


![\begin{gathered} c^2\text{ = 9+25 = 34} \\ c\text{ = }\sqrt[]{34} \\ c\text{ = 5.83} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ph8aadsitzll6fejuamdyeh69y99ggttki.png)
The equation becomes: