The total number of pieces in the domino is 28.
a)
The number of pieces that have an odd number of dots is 12, so the probability of choosing a piece with an odd number of dots is:
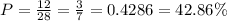
b)
The number of pieces that have 2 dots is 2, so:
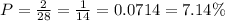
c)
The number of pieces that don't have 7 dots is 25, so:
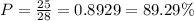
d)
The number of pieces that have at most 8 dots is 22, so:
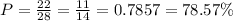
e)
The number of pieces that have more than 10 dots is 2, so:
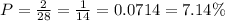
f)
The number of pieces that have a number of dots multiple of 4 is 7, so:
