To solve for the angles in a parallel line:
For a pair of parallel lines:
Corresponding Angles are equal m<1 = m<5 = 143°
Alternate Interior Angles are equal m<4 = m<6
Alternate Exterior Angles are equal m<2 = m<8
Consecutive Interior Angles add up to 180° m<3 + m<6 = 180
... then the lines are Parallel
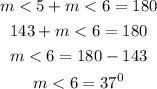
Therefore the consecutive interior angles add up to 180
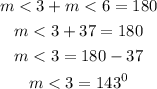
Therefore the consecutive interior angles add up to 180
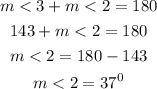
Hence the corresponding angle for m<3 = 143° and m<2 = 37°