Given:
The number of games played by 15 players are,
22, 123, 104, 150, 121, 162, 79, 151, 155, 142, 156, 144, 123, 87, 130.
The objective is to find five number summary for the number of games.
Step-by-step explanation:
The five number summary are minimum value, quartile 1, median, quartile 2 and maximum value.
Increasing order:
The increasing order of the given data is,
22, 79, 87, 104, 121, 123, 123, 130, 142, 144, 150, 151, 155, 156, 162.
Minimum and Maximum value:
By considering the increasing order of the data, the minimum value is 22 and the maximum value is 162.
To find median:
The median can be calculated as the middle term of total number of data.
Since, the total number of data is 15, which is odd, then the median can be calculated as,
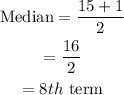
Thus, the 8th term of increased order is 130.
To find Q1:
The quartile 1 can be defined as the middle term of the left side of the median.
Since, the left side of the median contains 7 terms, which is odd, then the quartile 1 can be calculated as,
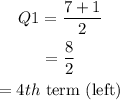
Thus, the 4th term on left side of median is 104.
To find Q3:
The quartile 3 can be defined as the middle term of the right side of the median.
Since, the right side of the median contains 7 terms, which is odd, then the quartile 3 can be calculated as,
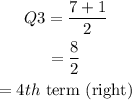
Thus, the 4th term on right side of median is 151.
Hence, the five number summary are,
Min: 22
Q1: 104
Median: 130
Q3: 151
Max: 162.