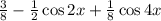Answer:
The expression becomes;
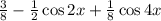
Step-by-step explanation:
Given the trigonometric expression;
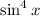
Simplifying and rewriting the expression;
Recall that;
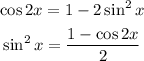
So, the expression becomes;
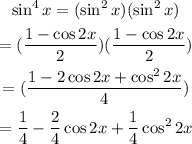
Also;
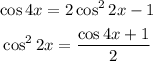
substituting to the above expression;
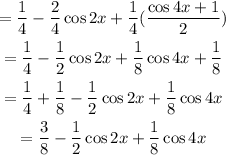
Therefore, the expression becomes;