Given the following expression:
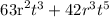
Let's determine its Greatest Common Factor (GCF):
The greatest number that we could divide both 63 and 42 is 21.
63 = (21 x 3), (9 x 7), (63 x 1)
42 = (21 x 2), (7 x 6), (42 x 1)
The greatest polynomial factor that we could divide both r^2 and r^3 is r^2.
r^2 = (r x r), (r^2 x 1)
r^3 = (r x r x r), (r^2 x r), (r^3 x 1)
The greatest polynomial factor that we could divide both t^3 and t^5 is t^3.
t^3 = (t x t x t), (t^2 x t), (t^3 x 1)
t^5 = (t x t x t x t x t), (t^4 x t), (t^3 x t^
With this, we can therefore say that the GCF of the given expression is 21r^2t^3. Factoring this out, we get:
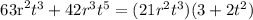
Therefore, the answer is letter A or the first option.