Answers: c = 17 and c = 18
==================================================
Step-by-step explanation:
Let's expand out the left hand side and rearrange terms like shown in the steps below.
(ax + 3)(bx + 4) = 6x^2 + cx + 12
ax(bx + 4)+3(bx + 4) = 6x^2 + cx + 12
abx^2 + 4ax+3bx + 12 = 6x^2 + cx + 12
abx^2 + (4a+3b)x + 12 = 6x^2 + cx + 12
Then equate the corresponding coefficients
- ab = 6 .... x^2 terms
- 4a+3b = c .... x terms
We'll use the fact that a+b = 5. Solving for 'a' gets us a = 5-b
Plug this into the equation dealing with the x^2 coefficients.
ab = 6
(5-b)b = 6
5b-b^2 = 6
0 = b^2-5b+6
b^2-5b+6 = 0
(b-3)(b-2) = 0
b-3 = 0 or b-2 = 0
b = 3 or b = 2
If b = 3, then a = 5-b = 5-3 = 2
If b = 2, then a = 5-b = 5-2 = 3
Therefore, the solutions to this system of equations
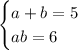
are (a,b) = (2,3) and (a,b) = (3,2)
In other words, the answer to the question "what two numbers multiply to 6 and add to 5?" is "2 and 3". The order doesn't matter which is why we can flip the 'a' and b values.
---------------------------------
Go back to 4a+3b = c which was us equating the x coefficients.
This is the same as c = 4a+3b
Plug in a = 2 and b = 3
c = 4a+3b
c = 4*2+3*3
c = 8 + 9
c = 17 is one possible value of c.
Now let's plug in a = 3 and b = 2
c = 4a+3b
c = 4*3+3*2
c = 12 + 6
c = 18 is the other possible value of c.