Answer:
See below for all the cube roots
Explanation:
DeMoivre's Theorem
Let
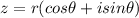 be a complex number in polar form, where
be a complex number in polar form, where
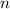 is an integer and
is an integer and
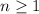 . If
. If
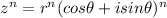 , then
, then
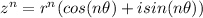 .
.
Nth Root of a Complex Number
If
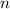 is any positive integer, the nth roots of
is any positive integer, the nth roots of
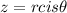 are given by
are given by
![\sqrt[n]{rcis\theta}=(rcis\theta)^{(1)/(n)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/36zrh2xhsy16a6ews8om.png) where the nth roots are found with the formulas:
where the nth roots are found with the formulas:
![\sqrt[n]{r}\biggr[cis((\theta+360^\circ k)/(n))\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/keo8r4kh1qjlg52qv3tr.png) for degrees (the one applicable to this problem)
for degrees (the one applicable to this problem)
![\sqrt[n]{r}\biggr[cis((\theta+2\pi k)/(n))\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/zhl0gu4gcxgmkzoorr8z.png) for radians
for radians
for

Calculation
![z=27(cos330^\circ+isin330^\circ)\\\\\sqrt[3]{z} =\sqrt[3]{27(cos330^\circ+isin330^\circ)}\\\\z^{(1)/(3)} =(27(cos330^\circ+isin330^\circ))^{(1)/(3)}\\\\z^{(1)/(3)} =27^{(1)/(3)}(cos((1)/(3)\cdot330^\circ)+isin((1)/(3)\cdot330^\circ))\\\\z^{(1)/(3)} =3(cos110^\circ+isin110^\circ)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ncims2cg459p6km5vn4g.png)
First cube root where k=2
![\sqrt[3]{27}\biggr[cis((330^\circ+360^\circ(2))/(3))\biggr]\\3\biggr[cis((330^\circ+720^\circ)/(3))\biggr]\\3\biggr[cis((1050^\circ)/(3))\biggr]\\3\biggr[cis(350^\circ)\biggr]\\3\biggr[cos(350^\circ)+isin(350^\circ)\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/wd39lnd6e6arrjjzgn7k.png)
Second cube root where k=1
![\sqrt[3]{27}\biggr[cis((330^\circ+360^\circ(1))/(3))\biggr]\\3\biggr[cis((330^\circ+360^\circ)/(3))\biggr]\\3\biggr[cis((690^\circ)/(3))\biggr]\\3\biggr[cis(230^\circ)\biggr]\\3\biggr[cos(230^\circ)+isin(230^\circ)\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/d0drq0f7gu1hi7u1rvdk.png)
Third cube root where k=0
![\sqrt[3]{27}\biggr[cis((330^\circ+360^\circ(0))/(3))\biggr]\\3\biggr[cis((330^\circ)/(3))\biggr]\\3\biggr[cis(110^\circ)\biggr]\\3\biggr[cos(110^\circ)+isin(110^\circ)\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/7nwwbs058qdxdxpsl6rc.png)