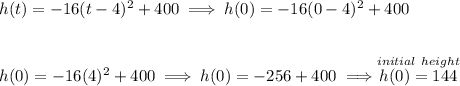Check the picture below.
well, since h(t) is already in vertex form, well hell we pretty much can see the vertex right off

now, when does it start above the ground?
well, from the picture below, notice, the initial height happens at 0 seconds, namely when t = 0, well, let's set it to 0.